Sesiones de grupo grande: Tema 8

TEMA 8: MEDIDAS DE TENDENCIA CENTRAL,POSICIÓN Y DISPERSIÓN

Además de las tablas y los gráficos podemos resumir una serie de observaciones mediante "estadísticos": "función de los datos observados". Solo se aplican a variables cuantitativas continuas (edad, peso, tiempo...).

Hay varios grandes tipos de medidas estadísticas:

MEDIDAS DE TENDENCIA CENTRAL

•        MEDIA: (media aritmética o simplemente media). Es el promedio aritmético de las observaciones, es decir, el cociente entre la suma de todos los datos y el numero de ellos.

•        MEDIANA (Me):es el valor que separa por la mitad las observaciones ordenadas de menor a mayor, de tal forma que el 50% de estas son menores que la mediana  y el otro 50% son mayores. Si el número de datos es impar la mediana será el valor central, si es par tomaremos como mediana la media aritmética de los dos valores centrales.

• 
  
•        MODA (M0): es el valor de la variable que más veces se repite, es decir, aquella cuya frecuencia absoluta es mayor. No tiene porque ser única.

MEDIDAS DE POSICIÓN O CUARTILES

-          Percentiles:

o   Dividen la muestra ordenada en 100 partes.

o   El valor del P₅₀ corresponde al valor de la mediana.

Ejemplo: el percentil de orden 15 deja por debajo al 15% de las observaciones, y por encima queda el 85%.

-          Deciles:

o   Dividen la muestra ordenada en 10 partes.

o   El decil “i” (D_i), es aquél valor que, ordenadas las observaciones en forma creciente, el i/10% de ellas son menores que él y el (100-i)/10% restante son mayores.

o   El valor del D₅ corresponde al valor de la mediana y, por tanto, al del P₅₀.

-          Cuartil:

o   Dividen la muestra ordenada en 4 partes.

MEDIDAS DE DISPERSIÓN

Las medidas de dispersión nos dicen hasta que punto estas medidas de tendencia central son representativas como síntesis de la información. Las medidas de dispersión cuantifican la separación, la dispersión, la variabilidad de los valores de la distribución respecto al valor central.

•        Varianza ( s2 ): es el promedio del cuadrado de las distancias entre cada observación y la media aritmética del conjunto de observaciones.

•        Desviación típica (S): La varianza viene dada por las mismas unidades que la variable pero al cuadrado, para evitar este problema podemos usar como medida de dispersión la desviación típica que se define como la raíz cuadrada positiva de la varianza

•        Recorrido o rango muestral (Re). Es la diferencia entre el valor de las observaciones mayor y el menor.  

Re = xmax - xmin

•        Desviación media: media artimética de las distancias de cada observación con respecto a la media de la muestra.

·         Recorrido intercuartílico: Diferencia entre el tercer y el primer cuartil = lQ₃-Q₁l

·         Coeficiente de variación: Es una medida de dispersión relativa (adimensional) ya que todas las demás se expresan en la unidad de medida de la variable. Nos sirve para comparar la heterogeneidad de dos series numéricas con independencia de las unidades de medidas. Se expresa sin unidades. 

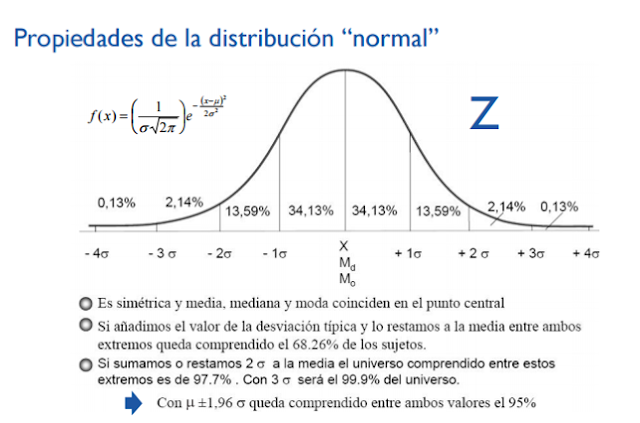
DISTRIBUCIONES NORMALES

ASIMETRÍA Y CURTOSIS

 - Coeficiente de asimetría de una variable: grado de asimetría de la distribución de sus datos en torno a su media, cuanto más asimétrica sea, valores más diferentes encontraremos. Es adimensional.

ASIMETRÍA

Los resultados pueden ser los siguientes:

-          g1=0 (distribución simétrica; existe la misma concentración de valores a la derecha y a la izquierda de la media).

-          g1>0 (distribución asimétrica positiva; existe mayor concentración de valores  a la derecha de la media que a su izquierda).

-          g1<0 (distribución asimétrica negativa; existe mayor concentración de valores a la izquierda de la media que a su derecha).

CURTOSIS O APUNTAMIENTO DE LA CURVA

Este sirve para medir el grado de concentración de los valores que toma en torno a su media. 

    Se definen 3 tipos de distribuciones según su grado de curtosis:

•       Distribución mesocúrtica: presenta un grado de concentración medio alrededor de los valores centrales de la variable (el mismo que presenta una distribución normal). 

•       Distribución leptocúrtica: presenta un elevado grado de concentración alrededor de los valores centrales de la variable. 
• 
  
•       Distribución platicúrtica: presenta un reducido grado de concentración alrededor de los valores centrales de la variable.

TIPIFICACIÓN DE LOS VALORES Y SU RELACIÓN CON LA CAMPANA DE GAUSS

La tipificación nos permite conocer si el valor corresponde o no a esa distribución con frecuencia.

Trabajamos con una variable continua que:

 - Sigue una distribución normal.

 - Tiene más de 100 unidades.

Ejemplo:

Para la tipificación necesitamos una tabla con los valores ya determinados. Yo os la facilito: